图计算常用算法
图算法的典型操作
关于一些常见图算法的调研与学习。
常用图算法
PageRank
背景
- 既考虑入链数量,又考虑了网页质量因素,二者相结合 数量与权重的结合
- 算法与主题无关,因为PR值是根据图计算出来的
算法原理
基本思想
A有链接指向B,表明A认为B比A重要。A将自身权重分配一部分给B。
$W(B)=W(A)/N$ W(A) 是A的PR值,W(B)是A 分配的权重,N是A的出链数
PageRank公式修正
存在出链为0的孤立网页,增加阻力系数q ,一般取q=0.85,其意义是用户有1-q的概率不点击此页面上面的所有链接。同时还有随机直接跳转的概率,如直接输入网址,点击书签等。完整公式如下:

Connected component
- 定义
- 连通分支:图中,某个子图的任意两点有边连接,而子图之间无边连接
- 问题:cc是寻找连通分支的算法??
- 通过BFS、DFS算法的便利就可以找到连通分支,每个白色节点开始的就是一个连通分支。
- 常见算法
- DFS
- 原理:访问某个顶点后只有当某个节点是叶结点后才会访问其余相邻节点。
- 步骤:
- 选择一个结点作为起始结点,标记为灰色
- 从该节点的邻居结点中选择一个结点,标记为灰色,继续这个操作
- 当选中的结点时叶子结点时,将其涂黑并返回到上一个父节点。
- 重复2,3直到所有结点都被访问。
- BFS (DFS,BFS不是图的遍历算法吗)。
- 原理:在进一步遍历中顶点之前,先访问当前结点的所有邻接结点。
- 步骤:
- 选择一个顶点作为起始节点,放入队列,标记为灰色,其余标记为白色
- 寻找队列首部结点的所有邻居节点,将其放入队列中并标记为灰色,将队列首部结点出队,并标记为黑色
- 重复2步骤,直到队列中的节点全部为空。
- DFS
SSSP (single-source shortest paths)
- 单独的起点与目标点之间最短路径的计算。起点固定,寻找与其他所有结点之间的最短路径。包括单源单汇,单源多汇
- 常见算法
- Dijkstra
- 步骤
- 将所有顶点分成两个集合A、B,其中集合A表示已经求得从V0出发的最短路径的顶点集合,集合B为为待求解的顶点集合。初始时有A={V0}
- 将集合A与集合B相连的边(A中的所有结点与B中所有的结点形成的边)按照从V0出发的最短权重和递增次序排序,取最短的边,将该条边在集合B中所对应的顶点加入到集合A中
- 重复第二步,直至B为空集。
- 总结:
- 最短中的最短:每次迭代时比较的是当前状态下以V0为起点,A中顶点为中间点的到各顶点之间的最短路径权重,最后再选择在当前所有最短路径中路径最短的一个顶点加入A。也就是说每次加入A集合的点是最短路径中的最短。
- 给定目标点,在每次迭代时,并不知道能否到达最后的目标点,所以把到所有结点的最短距离都算出来了。
- 步骤
- Dijkstra
Betweenness Centrality(中介中心性)
定义 :中心性用来衡量节结点的重要性。Betweenness Centrality :考虑的是该节点出现在其他两节点之间的最短路径上的比率。
思想:如果一个成员位于其他成员的多条最短路上,那么该成员就是核心成员,就具有较大的中介中心性。
步骤
其中
 表示的是节点s和t之间的最短路径的数量,而
表示的是节点s和t之间的最短路径的数量,而 是最短路径中经过节点v的数量。
是最短路径中经过节点v的数量。计算各个点对之间最短路径的长度和条数,用于计算pair-dependencies: δst(v) =σst(v)/σst
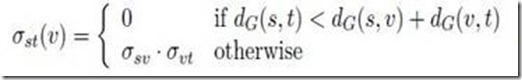
对于每个节点,累积属于自己的pair-dependencies

LBP算法(Local Binary Pattern, 局部二值模式)
定义:LBP是一种用来描述图像局部纹理特征的算子。
- 原始的LBP算子定义为在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0

作用是进行特征提取,而且,提取的特征是图像的纹理特征,并且,是局部的纹理特征.
改进版本
- 原型LBP算子
- LBP等价模式
最小生成树
- 定义:无环连通图,图中所有结点均参与,所有边的权重加起来最小。
- 算法
- Prim算法
- 步骤:设N=(V,{E})是连通网, TE是N上最小生成树中边的集合
- 初始令U={u0},(u0V), TE=φ
- 在所有uU,vV-U的边(u,v)E中,找一条代价最小
的边(u0,v0), 并保证不形成回路 - 将(u0,v0)并入集合TE,同时v0并入U
- 重复上述操作直至U=V为止,则T=(V,{TE})为N的
最小生成树
- 总结:每次迭代加入所有连通边中权值最小的。
- 步骤:设N=(V,{E})是连通网, TE是N上最小生成树中边的集合
- Prim算法
三角计数
- 定义:寻找无向图中的所有三角形
- 步骤
- 建立邻接表:
- 如果A-B & A < B,则将B加入A的邻接表 如果A-B & B < A,则将A加入B的邻接表 A<B比较的是id
- 遍历每个节点,对于结点A,遍历A邻接表中的结点,如果邻接结点B,C两两之间存在边,则A、B、C三者之间存在三角形
- 建立邻接表:
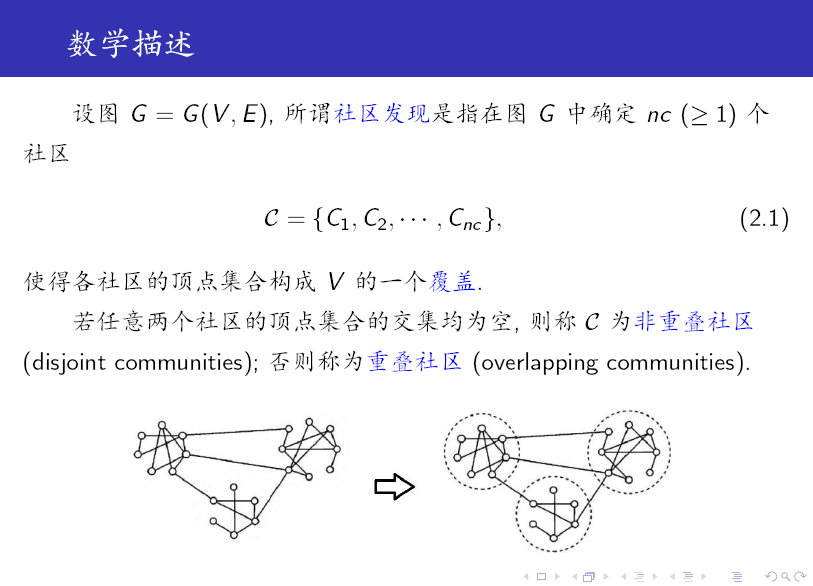
社区发现
社区定义:同一社区内的节点与节点之间的连接很紧密,而社区与社区之间的连接比较稀疏。社区是一个子图
数学描述:
衡量标准:模块度
- 计算公式
常见算法
- GN算法
- 思想:在一个网络之中,通过社区内部的边的最短路径相对较少,而通过社区之间的边的最短路径的数目则相对较多。从社区内部走大概率会走很多条边。
- 步骤
- 计算每一条边的边介数。边介数(betweenness):网络中任意两个节点通过此边的最短路径的数目。
- 删除边介数最大的边
- 重复(1)(2),直到网络中的任一顶点作为一个社区为止。
- 缺陷
- 不知道最后会有多少个社区
- 在计算边介数的时候可能会有很对重复计算最短路径的情况,时间复杂度太高
- GN算法不能判断算法终止位置
- LPA算法(标签传播算法)
- 思路
- 自己是什么标签,由邻居决定。邻居中什么标签最多,则此结点是什么标签
- 步骤
- 为所有结点指定一个唯一的标签
- 逐轮刷新所有结点的标签,直到达到收敛要求位置。刷新规则: 对于某一个节点,考察其所有邻居节点的标签,并进行统计,将出现个数最多的那个标签赋给当前节点。当个数最多的标签不唯一时,随机选一个。
- 思路
- GN算法
拓扑排序
- 定义 :拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面
- 步骤
- 从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出
- 从图中删除该顶点和所有以它为起点的有向边
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 BraveY!