数据预处理
数据预处理
为什么数据预处理
原始数据可能掺杂着噪音、空值或者不正确、不一致、充满冗余值等。没有高质量的数据,很难挖掘出高质量的规则,因此需要数据预处理。数据预处理主要有:数据清洗、数据集成、数据归约、数据离散等几个任务。
数据描述
得到一份数据后,需要先对数据进行一个大概的认识,主要从中心趋势和发散特征两方面统计进行描述。
中心趋势度量
平均值 mean
均值又分为:
算术均值
$\bar x=\frac{1}{n}\sum_{i=1}^{n}x_i$
加权均值
$\bar x= \frac{\sum_{i=1}^{n}w_ix_i}{\sum_{i=1}^{n}w_i}$
截尾均值 Trimmed mean
均值对极端数据比如离群点很敏感。因此截取高低两端的一部分数据后再计算均值,但是截去的部分不能太多不超过$20\%$
中位数 median
对于倾斜(非对称)数据,数据中心的更好度量是中位数。
假定数据有序,则当n为奇数时中位数是中间的值,当n为偶数的时候,中位数不唯一,可以是中间两个值和之间的任意值。如果属性是数值属性,那么一般约定取中间两个值的平均值。
众数 mode
另一种中心趋势的度量方法,众数是集合中出现最频繁的值。数据可能会有多个众数,如果最高频的值有多个的时候。如果每个数据值近出现一次,是没有众数的。
有一个、两个、三个众数的分别称为:单峰的(unimodal)、双峰的(bimodal)和三峰的(trimodal)
中列数 midrange
中列数是数据集的最大和最小值的平均值。
对称与倾斜
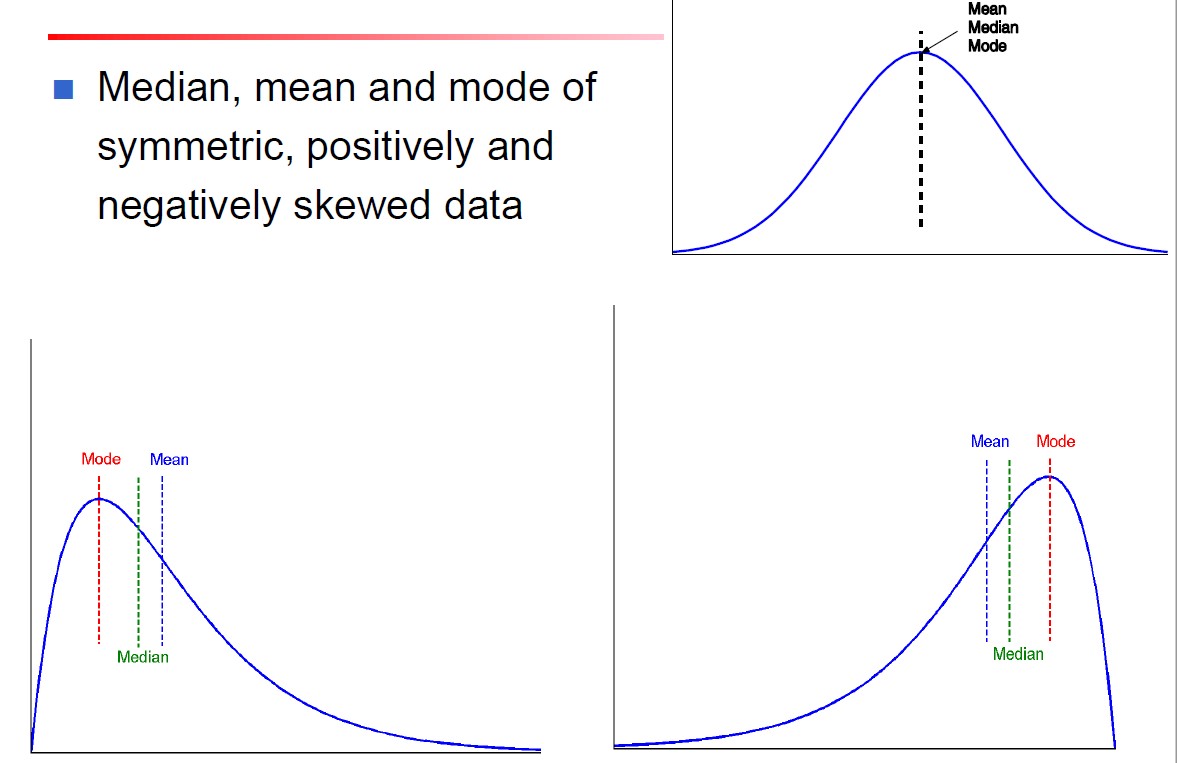
完全对称的数据分布的单峰频率曲线中,均值、中位数和众数三者是相同的中心值。
不对称的情况分为:
- 正倾斜:众数小于中位数
- 负倾斜:众数大于中位数
如下所示,最上方是对称的,左下是正倾斜的,右下是负倾斜的。
数据散布度量
极差、四分位数和四分位数极差
极差(range):最大值与最小值之差。
有序数据值下的数据集合的第k 个百分位数是具有如下性质的值x:数据项的百分之k 在x 上或低于x。在中位数M上或低于M 的值对应于第50 个百分位数。
四分位数将数据分为4段总共有3个四分位数,Q1是第25个百分位数,Q2即是Median是第50个百分位数,Q3是第75个百分位数。
100-分位数通常称为百分位数,它们把数据分成100个大小相等的连贯集。中位数、四分位数和百分位数是使用最广泛的分位数。
第一个和第三个四分位数之间的距离是分布的一种简单度量,它给出被数据的中间一半
所覆盖的范围。该距离称为中间四分位数极差(IQR):$IQR=Q_3-Q_1$
五数概括、盒图与离群点
离群点(Outlier):与$Q_1$或者$Q_3$这两个分位数的值超过$1.5IQR$
五数概括使用最小值、$Q_1$ 、中位数、$Q_3$、最大值来概述数据的中心与散布。
可以使用盒图来体现五数概括 。
- 盒的端点在四分位数上,使得盒的长度是中间四分位数区间IQR
- 中位数用盒内的线标记
- 盒外的两条线(称作胡须)延伸到最小(Minimum)和最大(Maximum)观测值。如果最大最小值超过$1.5IQR$,那么只延伸到这个部分。
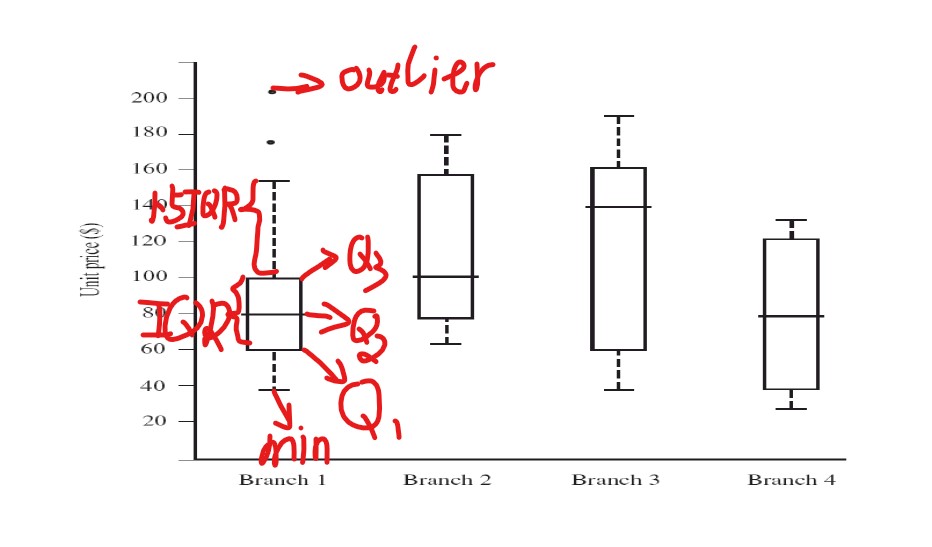
如上图所示,最大值超过了$1.5IQR$所以只延伸到了$1.5IQR$,而超过$1.5IQR$部分的被标记为离群点。
方差、标准差
方差Variance与标准差Standard deviation指出数据分布的散布程度。
总体方差的计算:$\sigma^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\mu)^2={\frac{1}{n}\sum_{i=1}^{n}x_i^2}-{\mu}^2$
样本方差的计算:$s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2={\frac{1}{n-1}(\sum_{i=1}^{n}x_i^2}-\frac{1}{n}\sum_{i=1}^{n}x_i^2)$
$\mu$是总体数据的平均值,而$\bar x$是总体数据中的一部分样本的均值,可以用样本的均值来估计总体的均值。样本方差是无偏估计的,样本方差与总体方差的差别
标准差是方差的平方根,就是$\sigma$或者s。它的性质是:
- $\sigma$度量关于平均值的发散,仅当选择平均值作为中心度量时使用。
- 仅当不存在发散时,即当所有的观测值都相同时,$\sigma=0$。否则,$\sigma>0$。
数据描述的图形表示
直方图
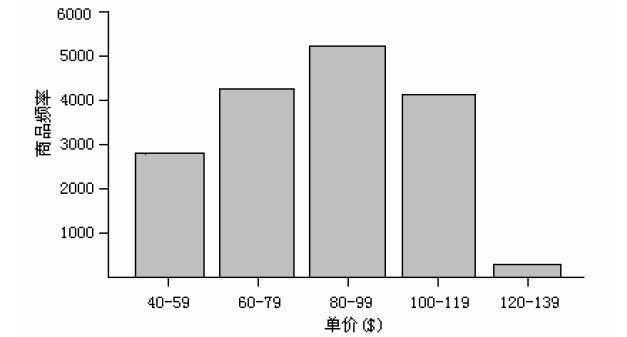
直方图Histogram 或者频率直方图Frequency histograms 针对单变量,对于比较单变量观测组,它可能不如分位数图、q-q 图和盒图方法有效。
分位数图
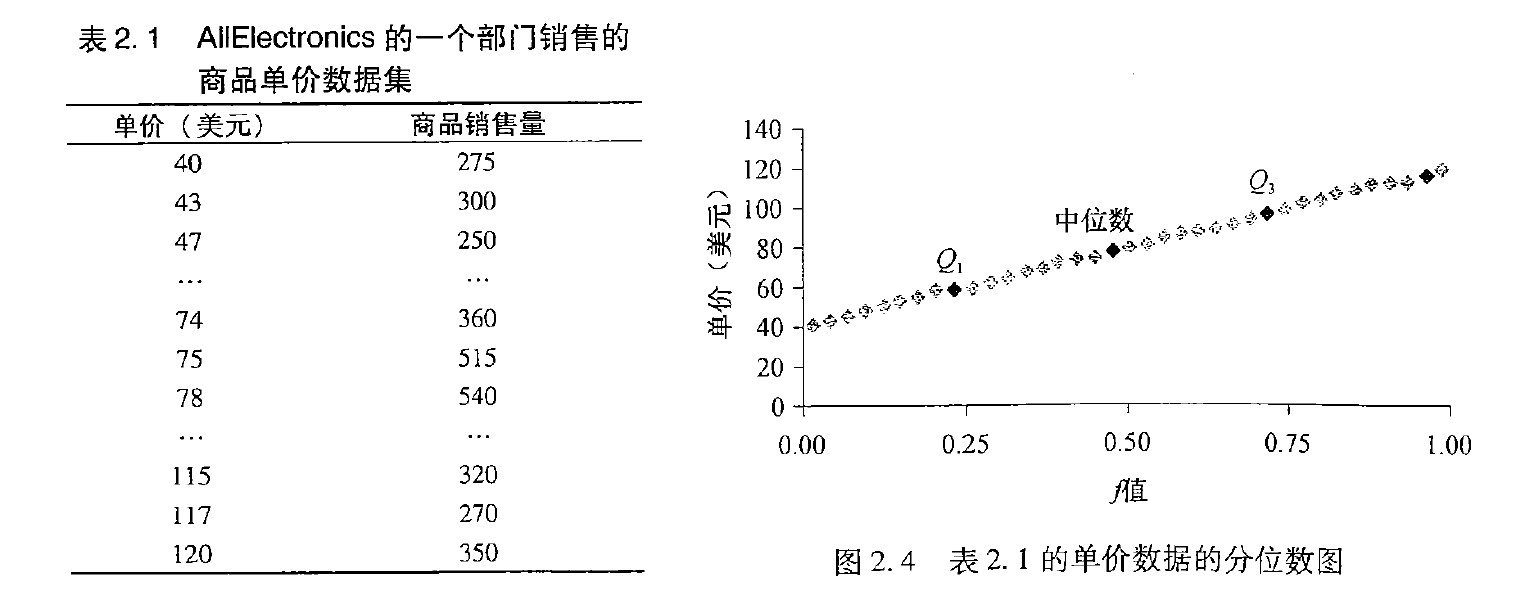
分位数图Quantile Plot每个观测值$x_i$与一个百分数$f_i$配对,指出大约$f_i \times 100\%$的数据小于值$x_i$,“大约”是因为可能没有一个精确的小数值$f_i$,使得数据的$f_i\%$小于或等于$x_i$。0.25 分位数对应于Q1,0.50 分位数对应于中位数,而0.75 分位数对应于Q3。
$f_i$的定义:$f_i=\frac{i-0.5}{N}$这些数由$\frac{1}{2N}$(稍大于0)到$1-\frac{1}{2N}$(稍小于1),以相同的步长1/n 递增。
分位数-分位数图
分位数-分位数图Quantile-Quantile Plot,或q-q 图对着另一个的对应分位数,绘制一个单变量分布的分位数。它是一种强有力的直观表示工具,使得用户可以观察从一个分布到另一个是否有漂移。![]https://res.cloudinary.com/bravey/image/upload/v1573992640/blog/Data%20Mining/qq_plot.jpg)
部门1的分布相对于部门2有一个漂移,更趋向于部门2,说明部门2的单价趋向于比部门1高。
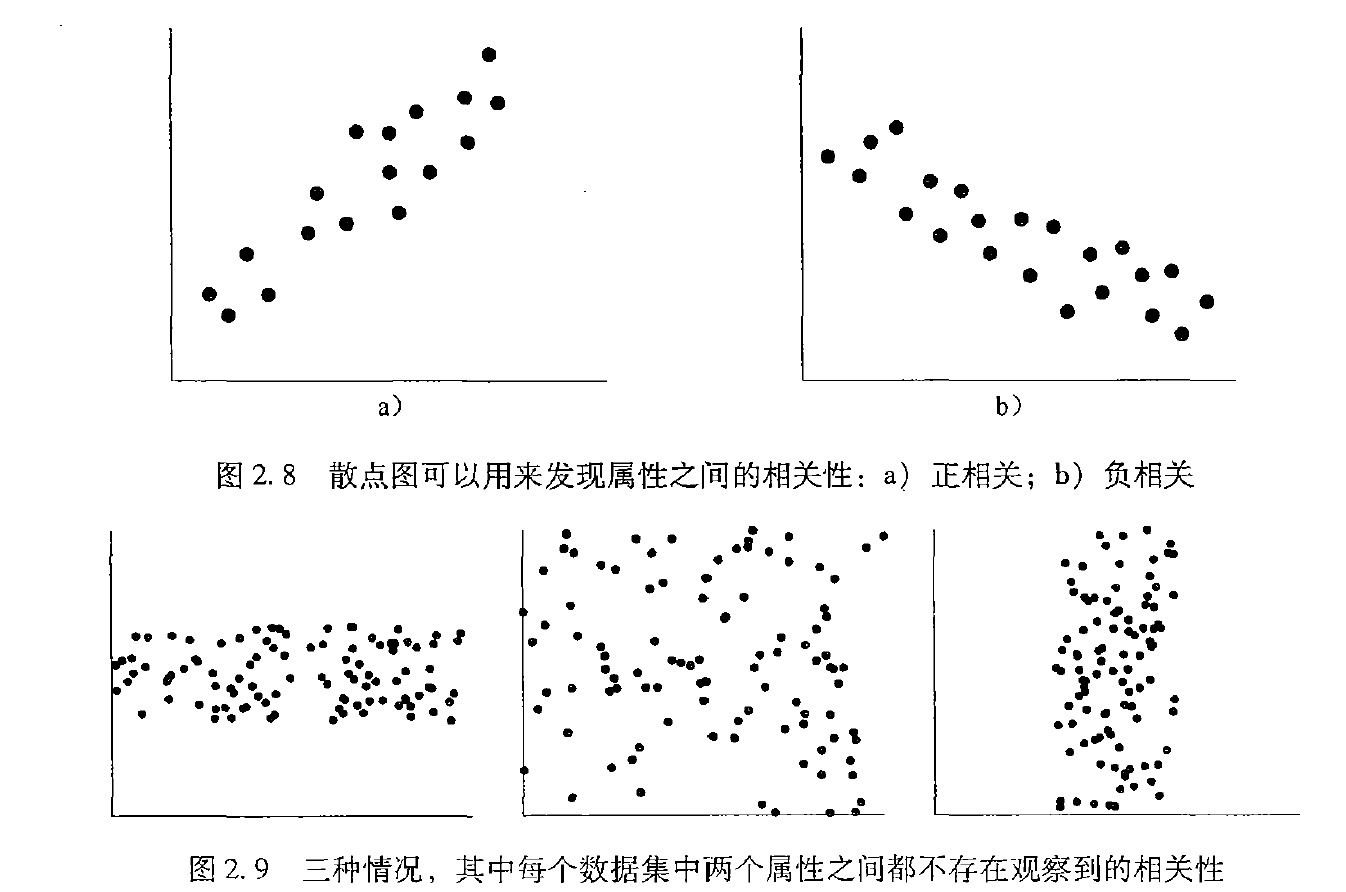
散点图
散点图(scatter plot)是确定两个量化变量之间看上去是否有联系、模式或趋势的最有效的图形方法之一。
它观察的是双变量,可以观察点簇和离群点,或者考察相关性。正相关x随着y的增加而增加,负相关x随着y的增长而减少。
数据清洗
缺失值
- 忽略元组
- 人工填写缺值
- 使用全局常量填充 :比如Unknown
- 所有样本的中心值填充:均值或者中位数 均值要求数据对称分布,倾斜分布用中位数
- 给定元组的分类相同的样本的均值或者中位数
- 最可能的值:使用贝叶斯推理、回归、决策数等进行预测。 前面几种是有偏的,这种方法最常用。
噪声数据
分箱
分箱方法通过考察“邻居”(即,周围的值)来平滑存储数据的值。存储的值被分布到一些“桶”或箱中。由于分箱方法导致值相邻,因此它进行局部平滑。
要求数据有序因此需要先进行排序,有三种方法:
- 箱均值光滑:箱中的每一个值被替换为箱中的均值
- 箱中位数光滑:箱中的每一个值被替换为箱中的中位数
- 箱边界光滑:边界为箱中的最大与最小值,每个值被替换为距离其最近的边界值。
而箱子的分法有等频(等深):每个箱子中的样本数目一样。等宽:按照取值范围将样本划分,每个箱子中的取值范围一致,比如样本数据取值为[0,10]那么可以按照等宽为2,把[0,2),[2,4)这样的取值范围来把样本划分到对应区间所在的范围中。

回归
用函数拟合数据来光滑数据,将离拟合曲线远的数据标记为噪声数据。
聚类
使用聚类分析后,检测出离群点,然后把离群点标记为噪声数据。
数据转换
归一化/规范化
最大-最小归一化
对原始数据进行线性变换,映射到新的区间[new_min, new_max]中去。这种方法保持了原始数据之间的联系。
z-score归一化
新的值使用均值和标准差进行映射。$\bar A$和$\sigma_A$ 分别是样本的均值和他的标准差。
小数定标归一化
小数定标归一化 Normalization by decimal scaling。移动原来的小数点的位置来进行归一化。
j是让$Max(|v_i’|<1)$的最小整数,比如如果是254,那么j取3就可以让其为0.254小于1。
冗余与相关性分析
一个属性可以由另外的属性导出,那么另外的属性就是冗余的。有些冗余可以通过相关性分析来检测
数值数据的相关系数
相关系数Correlation coefficient也称作皮尔森积矩系数Pearson’s product moment coefficient估计两个属性A,B的相关度。
$-1\le r_{A,B}\le 1$ ,$r_{A,B}>0$ A和B两个属性正相关,A的值随着B的值增长而增长。$r_{A,B}<0$为负相关,A的值随着B的值增长而减少。该值越大,一个属性蕴涵另一个的可能性越大。因此,一个很大的值表明A(或B)可以作为冗余而被去掉。如果结果值等于0,则A 和B 是独立的,它们之间不相关。可以参见前述的散点图。
分类数据的$\chi^2$相关检验
分类数据Categorical Data中,两类数据可以通过$\chi^2$卡方检验来发现它们的相关性。计算公式为:
$o_{ij}$ 是联合事件$(A_i,B_j)$的观测频度也就是实际频数,而$e_{ij}$ 是$(A_i,B_j)$的期望值。n是总的数据样本数。使用相依表来表示数据。

图中括号中的是每个单元的预测值。总共抽取1500个样本,因此n=1500。A类是否喜欢看小说有两类取值,B类性别也有两类取值,因此c=2,r=2。计算单元(男,小说)的预测值有:
其他几个单元的预测值都在括号中。因此可以计算出:
对于这个2*2的表,自由度为(2-1)(2-1)=1。对于自由度1,在0.001的置信水平下,查表得到拒绝假设的值是10.828。算出来的值大与它,因此认为性别和爱看小说不是独立的,是强相关的。
数据归约
数据归约技术 Data Reduction可以用来得到数据集的归约表示,它小得多,但仍接近地保持原数据的完整性。
分为:
- 维规约:降维
- 数量规约:用替代的、较小的的数据形式替换原始数据。比如只存放数据的模型参数
- 数据压缩:通过变换将原始数据压缩,不损失原来的信息叫做无损,否则是有损
维规约
小波变换
DWT)是一种线性信号处理技术,当用于数据向量D 时,将它转换成不同的数值向量小波系数D’。两个向量具有相同的长度。虽然变换后向量维度一样,但是可以仅存放一小部分最强的小波系数,就能保留近似的压缩数据。DWT提供比离散傅利叶DFT更好的有损压缩,DWT 将提供原数据更精确的近似。因此,对于等价的近似,DWT 比DFT 需要的空间小。不像DFT,小波空间局部性相当好,有助于保留局部细节。
该方法如下:
- 输入数据向量的长度L 必须是2 的整数幂。必要时,通过在数据向量后添加0,这一条件可以满足。
- 每个变换涉及应用两个函数。第一个使用某种数据平滑,如求和或加权平均。第二个进行加权差分,产生数据的细节特征。
- 两个函数作用于输入数据对,产生两个长度为L/2 的数据集。一般地,它们分别代表输入数据的平滑后或低频的版本和它的高频内容。
- 两个函数递归地作用于前面循环得到的数据集,直到结果数据集的长度为2。
- 由以上迭代得到的数据集中选择值,指定其为数据变换的小波系数。
主成分分析
主成分分析PCA 又称Karhunen-Loeve 或K-L 方法)搜索c 个最能代表数据的k-维正交向量;这里c ≤ k。这样,原来的数据投影到一个较小的空间,导致数据压缩。PCA 可以作为一种维归约形式使用。然而,不象属性子集选择通过保留原属性集的一个子集来减少属性集的大小。PCA 通过创建一个替换的、较小的变量集“组合”属性的本质。原数据可以投影到该较小的集合中。
详解的过程暂时不记录,查看模式识别的教材。只适用数值数据
属性/特征子集选择
也就是降维。使用压缩搜索空间的启发式的算法,典型的是贪心算法。每次找到一个局部的好的属性,剔除掉差的属性。
属性子集选择的基本启发式方法包括以下技术:
- 逐步向前选择:该过程由空属性集开始,选择原属性集中最好的属性,并将它添加到该集合中。
- 逐步向后删除:该过程由整个属性集开始。在每一步,删除掉尚在属性集中的最坏属性。
- 向前选择和向后删除的结合:向前选择和向后删除方法可以结合在一起,每一步选择一个最好的属性,并在剩余属性中删除一个最坏的属性。
- 判定树归纳:判定树算法,如ID3 和C4.5 。
数量规约
数据立方体集成
将数据整理成之前介绍过的数据立方体,把感兴趣的数据整理到基本立方体base cuboid上面。比如如果只关注每个季度的销售数据,那么可以将原来的每天的数据整理成每个季度的销售数据。这样就可以大大减少原来的数据量了。
回归
因为展开内容很多,只记录下有这些方法。当把数据拟合为某一种模型后只用记录这些模型的参数就可以了
- 线性回归
- 多元线性回归
- 对数线性模型
直方图
就是前面叙述的分箱的方法,使用一个桶来记录一个属性的频次。或者等宽的方法,用区间来记录每个区间中的频次。
聚类
聚类后,用数据的簇代表替换实际的数据。即只记录簇的中心点。
抽样
假定大的数据集D 包含N 个元组。我们看看对D 的可能选样。
简单选择n 个样本,不回放(SRSWOR):由D 的N 个元组中抽取n 个样本(n < N);其中, D中任何元组被抽取的概率均为1/N。即,所有元组是等可能的。
简单选择n 个样本,回放(SRSWR):该方法类似于SRSWOR,不同在于当一个元组被抽取后,记录它,然后放回去。这样,一个元组被抽取后,它又被放回D,以便它可以再次被抽取。
数据压缩
主要使用编码机制来进行压缩。包括字符串、音频、视频的压缩。
数据离散和概念分层
可以使用分箱来、聚类、决策树和相关分析来进行离散化。而对于标称数据可以进行概念分层,前面的数据立方体就是用的这个思路。
参考
《数据挖掘概念与技术》第3版 第三章数据预处理








