关联规则

基本概念

关联规则挖掘Association rules mining 挖掘出数据库中的频繁模式，频繁项之间的关联规则。

关联规则的形式为

$A\Rightarrow B[support=?, confident=?]$

规则的支持度support和置信度confident分别反映出规则的有用性和确定性。定义为：

$\begin{split} support(A\Rightarrow B)&=P(A\bigcap B)=\dfrac{count(A\bigcap B)}{count(total)}\\ confident(A\Rightarrow B)&=P(B|A)=\dfrac{count(A\bigcap B)}{count(A)} \end{split}$

$A\bigcap B$ 表示A事件和B事件一起发生。使用比例的支持度称为相对支持度，使用直接的次数称为绝对支持度。当规则满足设定的最小支持度和最小置信度的时候，规则是强关联规则。强关联规则并不一定是有趣的，使用提升度lift来衡量两个事件之间的相关性

$lift=\dfrac{P(A\bigcap B)}{P(A)P(B)}$

当lift大于1的时候表示A事件和B时间是正相关的，A随着B的出现而出现，lift为1的时候二者是独立的，lift小与1的时候二者负相关，意味着一个的出现可能导致另一个不出现。

关联规则的挖掘分为两步：

找出所有的频繁项集一个详细的出现次数大于最小支持度的次数则是频繁的
由频繁项集产生强关联规则

包含k个项的项集称之为k项集，如果集合中的项都是频繁的，那么集合称之为频繁k项集。

挖掘频繁项集的算法：Apriori和FP-Growth

Apriori

Apriori运用了一个先验规则：每个频繁项集的子集一定也是频繁的项集，使用这个规则来剪枝很多候选项（非频繁的子集其父集也一定不是频繁的所以可以不用考虑）。

算法步骤为：

首先扫描一次数据库得到频繁1项集
根据频繁k项集$L_k$生成频繁k+1项集（连接步和剪枝步组成）
- 先根据频繁k项集组合生成候选项
- 扫描数据库得到候选项的支持度
- 将不满足支持度的剔除
当没有频繁项或者候选项可以生成的时候终止

连接步

为了找出$L_k$ ,通过$L_{k-1}$与自身连接产生候选k项集的集合$C_k$设$l_1$和$l_2$ 是$L_{k - 1}$ 中的项集。记号$l_i[j]$表示$l_i$ 的第j 项（例如，$l_1[k-2]$表示$l_1$ 的倒数第3 项）。为方便计，假定事务或项集中的项按字典次序排序即$l_i[k]<l_i[k+1]$。执行连接$L_{k - 1}$ 与$L_{k - 1}$；其中，$L_{k - 1}$ 的元素是可连接的，如果它们前(k-2)个项相同；即，$L_{k - 1}$ 的元素l1 和l2 是可连接的，如果$(l_1 [1] = l_2 [1]) ∧ (l_1 [2]= l_2 [2]) ∧ … ∧ (l_1 [k-2] = l_2 [k-2]) ∧ (l_1 [k-1] < l_2 [k-1])$。条件$(l_1 [k-1] < l_2 [k-1])$是简单地保证不产生重复。连接$l_1$ 和$l_2$ 产生的结果项集是$l_1 [1] l_1 [2]… l_1 [k-1] l_2 [k-1]$。

举个例子假设频繁三项集有$l_1=[a,b,c], l_2=[a.b,d]$ 满足前缀相同最后一项不同所以可以产生候选的4项集：$C_4=[a,b,c,d]$ 把$l_2$的最后一项拼接到$l_1$后面。

剪枝步

$C_k$是频繁k项集的$L_k$的父集，可以扫描数据库来确定每一个$C_k$中的计数。但是$C_k$可能很大，所涉及的计算量也就很大。为压缩$C_k$，可以用以下办法使用Apriori 的先验性质：任何非频繁的(k-1)-项集都不是可能是频繁k-项集的子集。因此，如果一个候选k-项集的(k-1)项子集不在$L_{k - 1}$ 中，则该候选也不可能是频繁的，从而可以由$C_k$ 中删除。这种子集测试可以使用所有频繁项集的散列树(hash tree)快速完成。

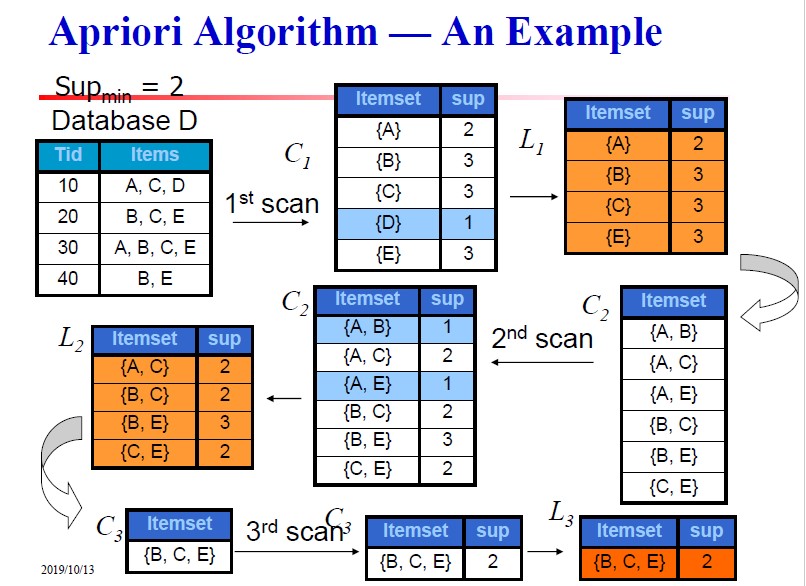
如上图的例子，第一次扫描得到频繁1项集的候选项$C_1$，然后根据支持度去除支持度计数小于2的$\{D\}$ 得到$L_1$，然后$L_1$中的各项进行连接步操作得到$C_2$，$C_2$ 执行剪枝步操作，因为所有项的子集都在$L_1$中所以不需要剪枝。进行第二次扫描得到$C_2$各项的支持度计数，然后把低于最小支持度的$\{A,B\},\{A,E\}$ 两项删除从而得到频繁2项集$L_2$。根据$L_2$执行连接步(只能由{B,C} 和{B, E}连接，其他的前缀不同)生成的$C_3=\{B,C,E\}$ 因为对应的3个子集{B,C},｛B,E｝和{C, E}都在频繁2项集中，所以也不需要剪枝。第三次扫描后得到$C_3$中各项的支持度计数，因为大于最小支持度计数，因此不需要删去得到了频繁3项集，因为频繁3项集只有一项无法进行连接步操作生成候选项集，所以算法终止。

产生关联规则

以上图为例，得到了频繁3项集$L_3={\{B,C,E\}}$后，对其所有非空子集$\{B\},\{C\},\{E\},\{B,E\},\{B,C\},\{C,E\}$ 计算对应的关联规则$l_1 \Rightarrow l_2\space or \space l_2 \Rightarrow l_1 $的置信度，如果满足最小置信度阈值则是强关联规则。

算法伪代码

改进算法

Partition ：仅扫描数据库两次
DHP：降低候选项的数目
DIC：降低扫描次数

评价

Apriori算法需要多次扫描数据库这带来的开销很大，同时会生成大量的候选项集并做子集测试也造成了很大的计算开销。

FP-Growth

频繁模式增长FP-Growth将代表频繁项集的数据库压缩到一颗频繁模式树Frequent Patterns (FP树)中。

FP树的构建

首先扫描一次数据库，找到频繁一项集。
根据支持度计数降序排列频繁项记为L
创建一个根节点，并标记为null
再次扫描数据库，将每个事务按照L中的顺序排列。为每个事务新建一个分支
- 如果事务中的项已经在分支中，则分支上的节点计数+1
- 如果项不在分支中，则在前缀路径下新建一个节点，计数为1
建立一个项头表把FP树中的每一项的节点相连。

FP树

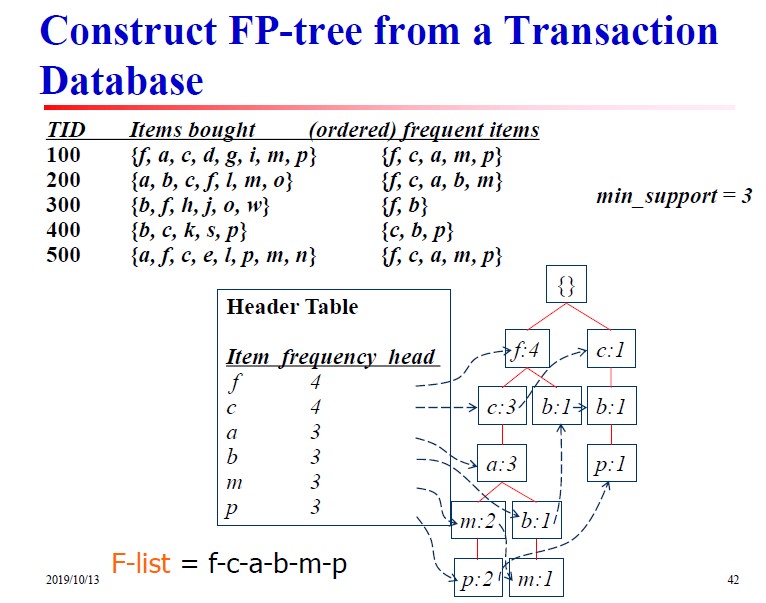
以上图为例，第一次扫描后得到的频繁一项集为$L_1=\{f:4,c:4,a:3,b:3,m:3,p:3\}$ 已经按照支持度计数降序排列为F-list。第二次扫描数据库，并按照F-list的顺序将每个事务排列（注意：低于支持度计数的项已经被删除了）。建立一个根节点并标记为null,第一个事务是$\{f,c,a,m,p\}$

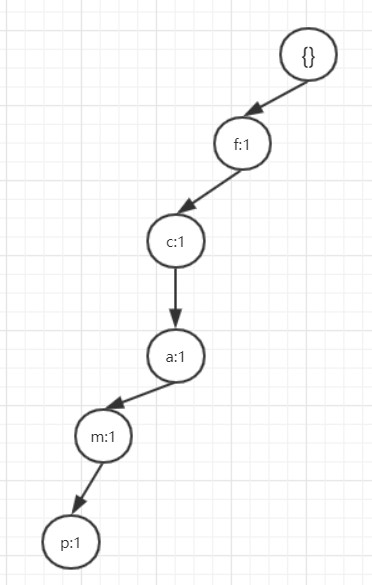
因为是第一个事务所以没有前缀路径可以共用，每个项都需要建立一个节点。第二个事务是$\{f,c,a,b,m\}$因为$\{f,c,a\}$ 是已经有的路径，所以对应的在这3个节点计数+1，$\{b,m\}$ 没有可以共享的路径所以需要新建立这两个节点。

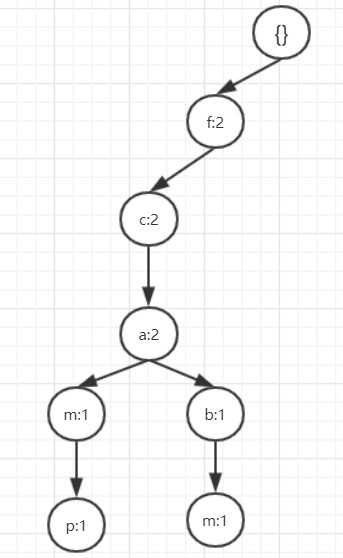
当所有事务都被加入到FP树后建立项头表将相同的项给链接起来就可以得到前面的完整的FP树。

条件模式基的构造

从项头表中具有最低的支持度计数的项开始构造每一个项的条件模式基Conditional Pattern Base。一个项的条件模式基定义为以这个项为后缀的前缀路径。

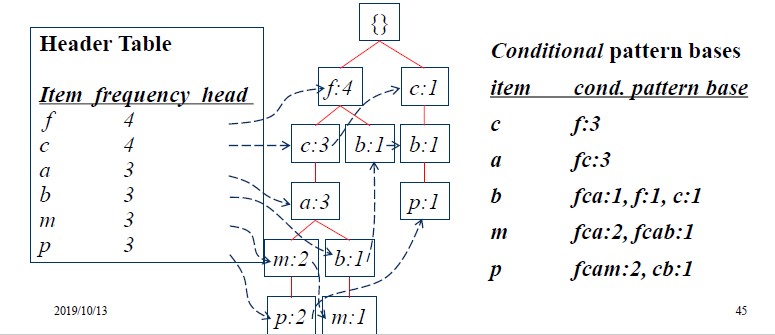
以上图为例，先构造p的条件模式基，在FP树中，以p为后缀的路径为$fcam:2 和cb:1$ 后面的计数是根据每条路径的后缀的计数来确定的因此第一条$fcamp$路径的计数为2而$cbp$为1。依次可以得到每个项的条件模式基。对每一个项的条件模式基都可以按照前述的FP树的构造方法得到其对应的条件FP树。以m的条件模式基构建的条件FP树为：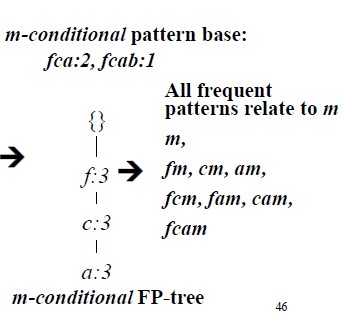

因为b的支持度计数只有1所以删去。

频繁模式的产生

根据条件FP树的路径产生频繁模式，路径的每个非空子集与对应的项组合产生对应的频繁模式。比如m的FP树路径为：$\{fca\}$ 对应的子集有$\{f\},\{c\},\{a\}, \{f,c\},\{f,a\},\{a,c\},\{f,c,a\}$与m组合后得到的频繁模式有：$\{f,m\},\{c,m\},\{a.m\}, \{f,c,m\},\{f,a.m\},\{a,c,m\},\{f,c,a,m\}$