线性判别函数

模式识别与机器学习第三章的笔记。

线性判别函数

n维线性判别函数的一般形式

一个n维线性判别函数的一般形式：

$d(x)=w_1x_1+w_2x_2+\dots+w_nx_n+b=W_0^tx+b$

其中$W_0=(w_1,w_2,\dots,w_n)^T$称为权向量，如果把b也加入到权向量则$d(x)=W^Tx$ 其中$x=(x_1,x_2,\dots,x_n,1)$ 称为增广模式向量 (b对应的特征维度取值为1),而权向量也对应的加入b$W=((w_1,w_2,\dots,w_n,b)^T)$ 称为增广权向量。

两类情况

样本如果只有两类$\omega_1,\omega_2$则可以只用一个线性判别函数进行判别：

$d(x)=W^Tx=\left\{ \begin{array}{**lr**} >0 & if\;x\in \omega_1\\\\ \le0& if\;x\in\omega_2 \end{array} \right.$

多类情况

多类情况1

用线性判别函数将属于$ω_i$类的模式与不属于$ω_i$类的模式分开，其判别函数为：

$d(x)=W^Tx=\left\{ \begin{array}{**lr**} >0 & if\;x\in \omega_i\\\\ \le0& if\;x\notin\omega_i \end{array} \right.$

这种情况称为$w_i/\bar w_i$两分法，即把M类多类问题分成M个两类问题，因此共有M个判别函数 ，每一类都有一个自己的判别函数，只负责把这一类给判别出来。

把样本点带入所有的判别函数，有且只有一个判别函数判定这个样本值为正，其他判别函数都判定为负，则分类成功，否则分类失败。分类失败的区域称为不确定区域

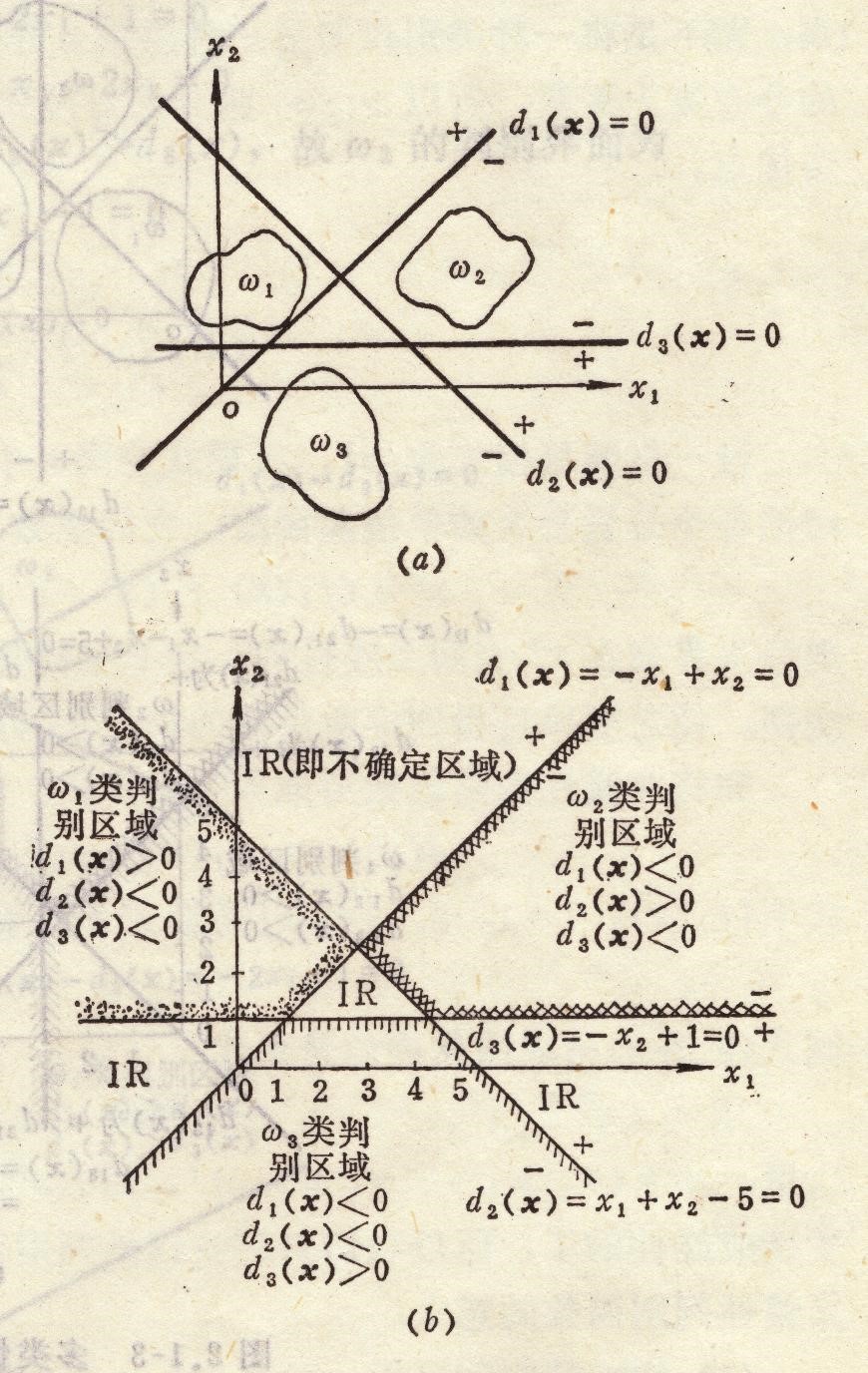
判别界面不穿过类，每个判别界面可以准确的判别出一类样本。

不确定区域在图上就是除了能判定3个类别以外的区域，包括三条直线围成的中间的三角形，和三个角延伸出来的区域。

多类情况2

每个判别函数去划分一对样本，一个判别界面只能分开两种类别，称为$\omega_i/\omega_j$两分法。判别函数为：

$d_{ij}(x)=W_{ij}^Tx$

其中当$d_{ij}x>0 \quad\forall j\neq i$ 则将样本划入$\omega_i$类。比如$d_{12}(x)$只能判别是第一类还是第二类样本。

重要的性质：$d_{ij}=-d_{ji}$

对于M类模式，总共需要M(M-1)/2个判别函数。

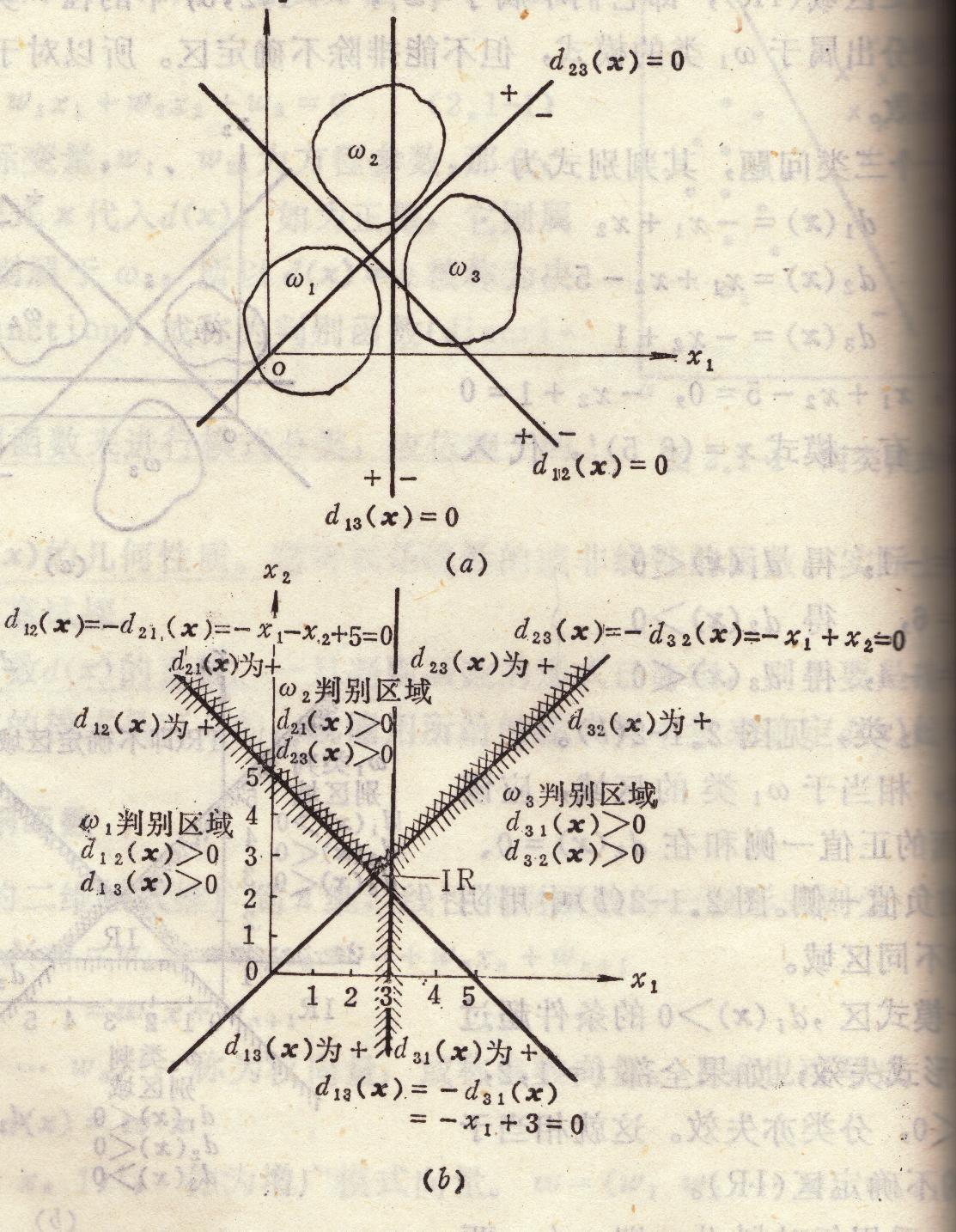
判别界面会穿过类，因此一个单独的判别函数无法准确的判别出一个完整无误的类，所以需要多个判别函数来辅助判别。只有所有的判别函数都判别这个样本都属于同一类，才能确定其属于这一类。

需要依次根据这一类$\omega_i$的所有判别函数$d_{i1},d_{i2},\dots,d_{ij}$ 都得到正值，才判断其为$\omega_i$类。

不确定区域只剩下中间围成的三角区域了。因此多类情况2对模式是线性可分的可能性比多类情况1更大一些。

多类情况3

是多类情况2没有不确定区域的特例。特例引入的条件是：

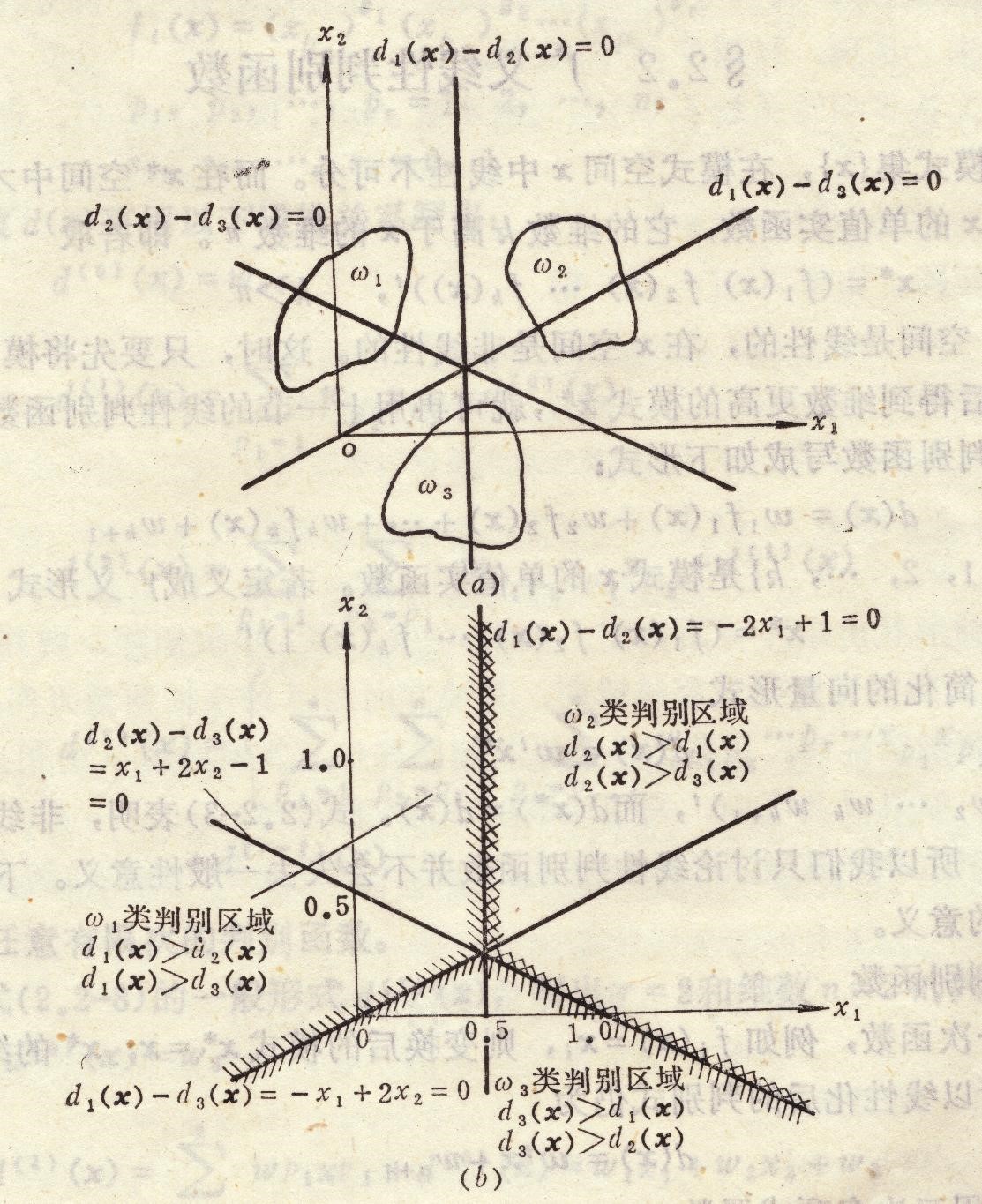
$d_{ij}(x)=d_i(x)-d_j(x)=(W_i^T-W_j^T)x$ 因此当$d_{ij}(x)>0$有$d_i(x)>d_j(x) \quad\forall j\neq i$ 这时不存在不确定区域，判别界面相交于一点。此时M类情况，对应有M个判别函数。

根据上面的条件，只有当$d_i(x)$大于所有$d_j(x)$的时候，才会有所有的$d_{ij}(x)>0$。因此把样本带入所有的判别函数，选择值最大的一个作为划分的类。

该分类的特点是把M类情况分成M-1个两类问题。

广义线性判别函数

出发点

线性判别函数简单，容易实现；
非线性判别函数复杂，不容易实现；
若能将非线性判别函数转换为线性判别函数，则有利于模式分类的实现。

基本思想

如果在低维度中不是线性可分的（判别函数在低维度中是非线性的），将样本用非线性的变换（比如多项式）映射到能够线性可分的高维度中去，然后在高维度中用线性判别函数来分类。

对于原来的样本x向量，可以变换为：

$x^*=(f_1(x), f_2(x),\dots,f_k(x))^T, k>n$

总项数

对于n维x向量，若用r次多项式，d(x)的权系数的总项数为：

$N_w=C_{n+r}^{r}=\dfrac{(n+r)!}{n!r!}$

Fisher 线性判别

求一个投影后能够分开的权重法向量$W$,从d维空间变换到一维空间。

基本参量

d维x空间

样本的均值向量
样本类内离散度矩阵和总样本类内离散度矩阵
样本类间离散度矩阵

一维Y空间

样本的均值向量
样本类内离散度矩阵和总样本类内离散度矩阵

感知器

两类

使用误分类的样本点到判别平面的距离作为目标函数，要求最终下降到0，通过随机梯度下降法来进行优化。每次向输入的误分类点移动一步（加上对应的值），直到对于所有的样本点都可以正确分类。负梯度的方向就是样本向量的方向。

感知器的解存在很多，加上b偏置就是余量。距离理解成置信度

多类情况3

有多少类就有多少个判别函数，要求对于第i类样本其对应的$d_i(x)$判别函数一定最大的（不存在相等的），如果不是最大的则其对应的加上这个样本$x_i$超过的减去这个样本。

每一次同一个样本要带入所有判别函数，然后再对所有的判别函数进行调整。

梯度法

确定好了对误分类敏感的准则函数（目标函数），先对准则函数求得其梯度向量，对于误分类的样本点朝着负梯度方向来更新权重系数。

感知器算法选择准则函数是误分类点的函数间隔$y_i(wx_i+b)$

选择不同的准则函数，得到的梯度也是不一样的，因此权重的更新的值也不一样。

最小平方误差算法

最小平方误差(LMSE)算法，除了对可分模式是收敛的以外，对于类别不可分的情况也能指出来。

分类器的不等式方程

将所有样本增广后写入一个矩阵X，X是N*（D+1）的矩阵，每一行是一个具体的样本，N是总共的样本数，其中负类的样本乘以-1规范化，因此判别界面的要求是：$Xw>0$ 其中W是一个D+1维度的权向量，乘法得到的向量是一个N行的列向量，对应的是没一个样本的$w^Tx$ 。

H-K算法

求解的是$Xw=b$ 式子中$b=(b_1,b_2,\dots,b_n)^T$的所有分量都是正值。因为X是一个$N*(D+1)$ 通常行大于列的长方阵，属于超定方程，因此一般情况下，不存在确定解，但是可以求线性最小二乘解。

将b看作真实的值，因此平方误差就是$(w^Tx-b)^2$ 。

所以可以将准则函数定义为：

$J(w,x,b)=\dfrac{1}{2}\sum_{i=1}^{n}(w^Tx_i-b_i)^2=\dfrac{1}{2}\sum_{i=1}^{n}||w^Tx_i-b_i||^2=\dfrac{1}{2}(Xw-b)^T(Xw-b)$

势函数

非线性分类的方法。

判别函数由样本向量的势函数产生。每个样本点对应与一个位置所以对应一个势能。

在第k步迭代时的积累位势决定于在该步前所有的单独势函数的累加。

以K(x)表示积累位势函数，若加入的训练样本xk+1是错误分类，则积累函数需要修改，若是正确分类，则不变。

两类问题$\omega_1$的样本产生的势能为正，$\omega_2$样本产生的势能为负。

迭代的时候，只有错分的样本才会积累势能，正势能的如果被错分（带入积累势能函数中为负）则积累的势能需要加上这个点的势能。反之负势能的如果被错分（代入积累势能函数中为正），则积累势能减去这个点的势能。

积累势能函数由误分类的样本的势函数累加得到。

第一类势函数：可用对称的有限多项式展开。

$K(x,x_k)=\sum_i=1^m\phi_i(x)\phi_i(x_k)$

注意是先乘了再相加，第二项的$\phi_i(x_k)$可以理解成每个样本点对应的权重

最终的迭代关系为：

$d_{k+1}(x)=\sum_{i=1}^mC_i(k+1)\phi_i(x)\\ C_i(k+1)=C_i(k)+r_{k+1}\phi_i(x_{k+1})$

势函数确定了，每个样本都是同样的势函数形式，但是判别函数也就是积累势函数随着样本的加入而在不断的更新，特别是误分类的样本会更新势函数。

第二类势函数：选择双变量x和xk的对称函数作为势函数，即K(x, xk) = K(xk, x)，并且它可展开成无穷级数。如下三种势函数

$K(x,x_k)=e^{-\alpha||x-x_k||^2}\\ K(x,x_k)=\frac{1}{1-\alpha||x-x_k||^2} \quad \alpha >0\\ K(x,x_k)=\dfrac{sin\alpha||x-x_k||^2}{\alpha||x-x_k||^2}$